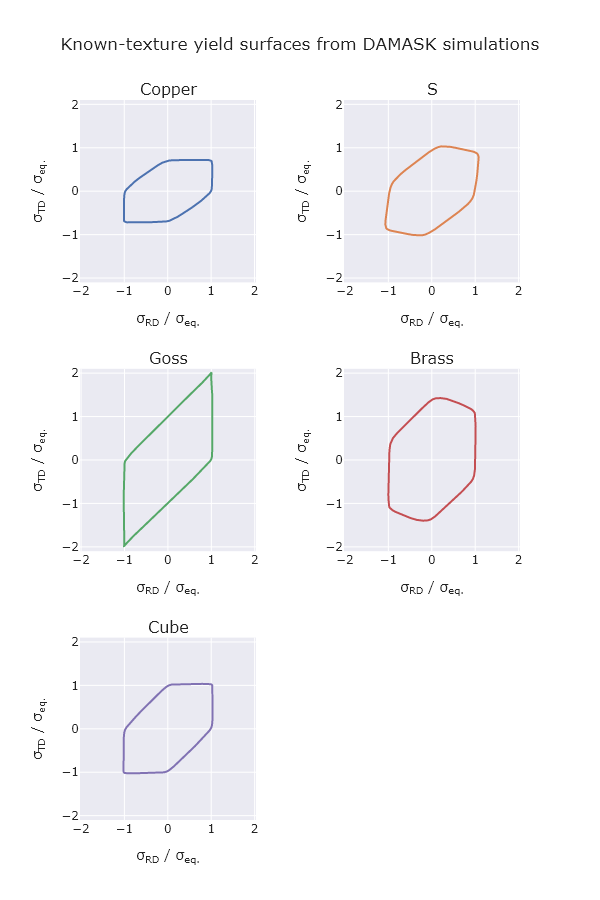
Simulating yield surfaces with DAMASK simulations#
This Jupyter notebook processes the results from the demo workflow simulate_yield_surface_2D, and generates a plot of yield surfaces for a range of known-textures (e.g. Cube, Goss, etc.).
from collections import defaultdict
import numpy as np
from IPython.display import Image
from plotly.subplots import make_subplots
from plotly.graph_objects import FigureWidget
import matflow as mf
Utility functions#
def get_hydrostatic_tensor(tensor):
"""Returns the hydrostatic tensor from an input stress strain tensor
Parameters
----------
tensor : ndarray of shape array (..., 3, 3)
Returns
-------
(..., 3, 3) array hydrostatic stress on the diagonal of tensor with 0 in shear values
"""
hydro = np.zeros_like(tensor)
hydro[..., [0, 1, 2], [0, 1, 2]] = (np.trace(tensor, axis1=-2, axis2=-1) / 3)[
..., None
]
return hydro
def get_von_mises(s, tensor):
"""Returns the equivalent value of stress or strain tensor
Parameters
----------
tensor : ndarray of shape (..., 3, 3)
Tensor of which to get the von Mises equivalent.
s : float
Scaling factor: 3/2 for stress, 2/3 for strain.
Returns
-------
Von Mises equivalent value of tensor.
"""
deviatoric = tensor - get_hydrostatic_tensor(tensor)
return np.sqrt(s * np.sum(deviatoric**2.0, axis=(-2, -1)))
def get_von_mises_stress(stress):
return get_von_mises(3 / 2, stress)
def get_von_mises_strain(strain):
return get_von_mises(2 / 3, strain)
def order_coplanar_points(points, normal, anticlockwise=True):
"""
Find the clockwise or anticlockwise ordering of a set of coplanar 3D points.
Parameters
----------
points : ndarray of shape (3, N)
The set of coplanar points (three-vector columns) whose ordering is to be found.
normal : ndarray of shape (3, 1)
Column three-vector representing the normal of the plane on which all points lie.
Returns
-------
Ordered indices of points according to a clockwise or anticlockwise direction when
looking in the opposite direction to `normal`.
"""
# Normalise `normal` to a unit vector:
normal = normal / np.linalg.norm(normal)
# Compute the centroid:
centroid = np.mean(points, axis=1)
# Get the direction vectors from each point to the centroid
p = points - centroid[:, np.newaxis]
# Use the first point as the reference point
# Find cross product of each point with the reference point
crs = np.cross(p[:, 0:1], p, axis=0)
# Find the scalar triple product of the point pairs and the normal vector
stp = np.einsum("ij,ik->k", normal, crs)
# Find the dot product of the point pairs
dot = np.einsum("ij,ik->k", p[:, 0:1], p)
# Find signed angles from reference point to each other point
ang = np.arctan2(stp, dot)
ang_order = np.argsort(ang)
if not anticlockwise:
ang_order = ang_order[::-1]
return ang_order
Processing functions#
def group_elements_by_texture(workflow, err_ids=None):
"""Group elements by the RVE texture."""
# TODO: speed up this sort of scenario (upstream dependencies inputs/ouputs
# retrieval; and could cache all elements first)
sim_elems_by_ori = defaultdict(list)
for elem in workflow.tasks.simulate_VE_loading_damask.elements:
if elem.index in (err_ids or []):
continue
gen_VE_elem = [
i
for i in elem.get_element_dependencies(as_objects=True)
if i.task.name == "generate_volume_element_from_voronoi"
][0]
sample_texture_elem = [
i
for i in gen_VE_elem.get_element_dependencies(as_objects=True)
if i.task.name == "sample_texture_from_model_ODF_mtex"
][0]
modal_ori_euler = sample_texture_elem.inputs.ODF_components.value[0][
"modal_orientation_euler"
]
sim_elems_by_ori[tuple(modal_ori_euler)].append(elem)
return sim_elems_by_ori
def get_stress_at_yield(VE_response, criterion=0.002):
stress = VE_response.value["phase_data"]["vol_avg_stress"]["data"][:]
plastic_strain = VE_response.value["phase_data"]["vol_avg_plastic_strain"]["data"][
:
]
plastic_strain_vM = get_von_mises_strain(plastic_strain)
yield_idx = (np.abs(plastic_strain_vM - criterion)).argmin()
stress_at_yield = stress[yield_idx]
return stress_at_yield
def get_yield_tensors(sim_elements, criterion=0.002):
yield_tensors = np.array(
[get_stress_at_yield(i.outputs.VE_response, criterion) for i in sim_elements]
)
# find where y-stress is closest to zero:
eq_stress_idx = np.abs(yield_tensors[:, 1, 1]).argmin()
eq_stress = np.abs(yield_tensors[eq_stress_idx, 0, 0])
# normalise by equivalent stress:
yield_tensors = yield_tensors / eq_stress
return yield_tensors
def plot_yield_surfaces(sim_elems_by_ori, texture_eulers):
nsubplots = len(sim_elems_by_ori)
ncols = 2
nrows = int(np.ceil(nsubplots / ncols))
fig = make_subplots(
rows=nrows,
cols=ncols,
subplot_titles=list(texture_eulers),
vertical_spacing=0.12,
horizontal_spacing=0.2,
)
fig.update_layout(
height=300 * nrows,
width=300 * ncols,
showlegend=False,
template="seaborn",
title_text="Known-texture yield surfaces from DAMASK simulations",
)
for i in range(1, nsubplots + 1):
fig.layout[f"yaxis{i}"].update(
scaleanchor=f"x{i}",
scaleratio=1,
range=[-2.1, 2.1],
title="σ<sub>TD</sub> / σ<sub>eq.</sub>",
)
fig.layout[f"xaxis{i}"].update(
title="σ<sub>RD</sub> / σ<sub>eq.</sub>",
)
for idx, (text_name, eulers) in enumerate(texture_eulers.items()):
elems = sim_elems_by_ori[eulers]
yield_tensors = get_yield_tensors(elems)
x = yield_tensors[:, 0, 0]
y = yield_tensors[:, 1, 1]
xy0 = np.array([x, y, np.zeros_like(x)])
order_idx = order_coplanar_points(xy0, np.array([0, 0, 1])[:, None])
order_idx = np.concatenate((order_idx, order_idx[0:1])) # close the loop
x = x[order_idx]
y = y[order_idx]
fig.add_scatter(x=x, y=y, row=(idx // 2) + 1, col=(idx % 2) + 1)
return fig
Load and process simulations#
TEXTURE_EULERS = {
"Copper": (90, 35, 45),
"S": (59, 37, 63),
"Goss": (0, 45, 90),
"Brass": (35, 45, 90),
"Cube": (0, 0, 0),
}
wk = mf.Workflow(r"/path/to/simulate_yield_surface_2D/workflow")
# simulate task element indices that failed
err_ids = (19,) # 19: out of memory
sim_elems_by_ori = group_elements_by_texture(workflow=wk, err_ids=err_ids) # ~ 1 min runtime
Plot yield surfaces#
fig = plot_yield_surfaces(sim_elems_by_ori, TEXTURE_EULERS)
fig.write_image("yield_surfaces.png")
Image("yield_surfaces.png")